While all comparison-based algorithms have a time complexity of O(nlogn) to sort n input elements, there are sorting algorithms running in linear time provided that some assumptions are verified. Counting sort is an algorithm that has a time complexity of O(n), assuming that each of the n input elements is an integer in the range 0 to k or has an integer key in that range. An important property of counting sort is that it is stable: elements with the same key appear in the output array in the same order as they do in the input array.
Counting the frequencies
Counting sort is based on the idea that the frequency of the keys can be used to determine the position of the input elements in the sorted output. According to the assumption that the keys are in the range 0 to k, the frequency of the keys can be easily computed using an integer array of size k+1 initialized with zeros. Since the i-th element of this array will be used to count the frequency of the key i, we can call it the counter array. We can fill the counter array with the actual frequencies of the keys iterating through the input array once and increasing the counter corresponding to the current input key.
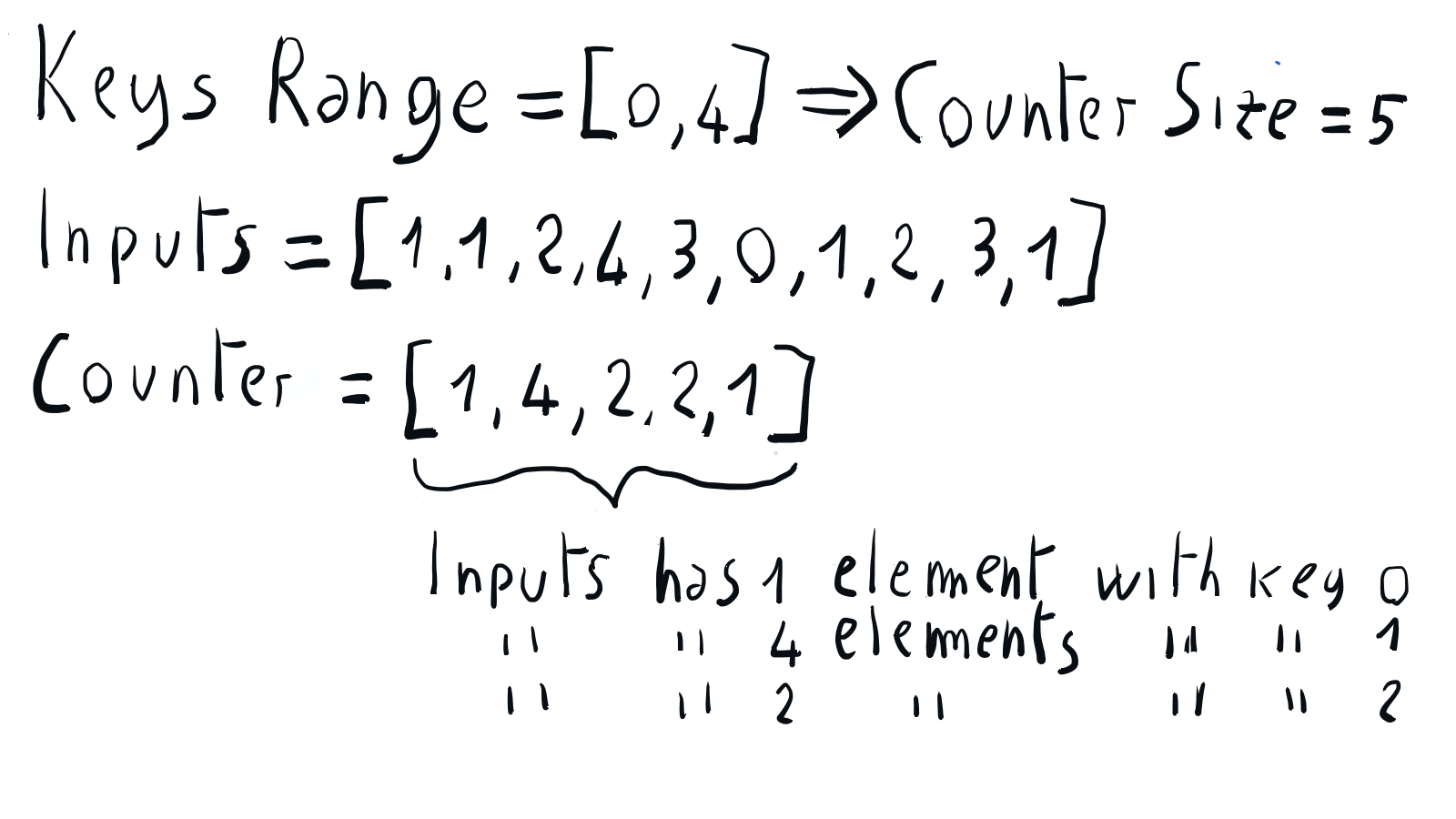
Building the sorted output
If there are only integer keys without attached values, it is trivial to build the sorted output. We can just iterate a second time through the counter array and fill the sorted output with the occurrences of each key.
void countingSort(vector<int>& nums, int maxKey) {
vector<int> counter(maxKey+1);
for (int num : nums) counter[num]++;
for (int i = 0, k = 0; i <= maxKey; ++i) {
for (int j = 0; j < cnt[i]; ++j) {
nums[k++] = i;
}
}
}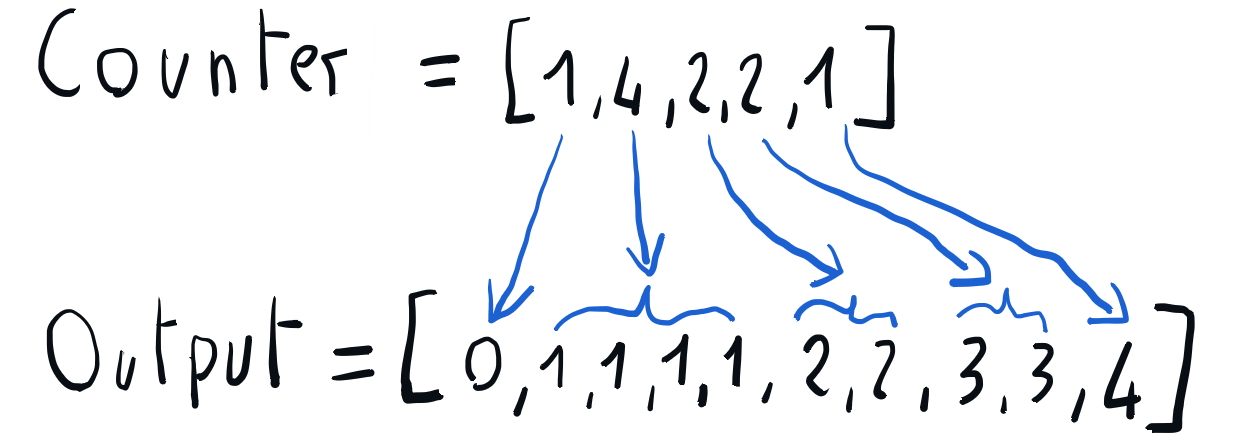
Introduce nextIndex array
If there are values attached to the integer keys, it is necessary to precompute the position in the output where each element from the input should go. We can use the counter array to build up another array that will track where the next occurrence of a key goes in the sorted output. We can call this array nextIndex because its i-th element represents the position of the next input element with key i in the sorted output. At the beginning, the position of the element with key i corresponds to the number of elements with key less than i. So we can fill the i-th element of the nextIndex array with the cumulative sum of the counter up to the index i-1.
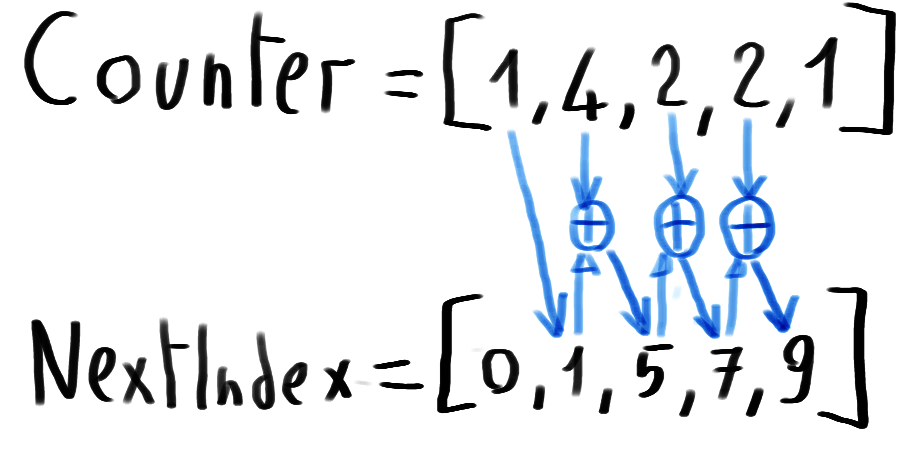
Building the sorted output using nextIndex
We can build the sorted output iterating through the input array and using the information in the nextIndex array to place each element directly into its position in the output array. Once every element is placed in its output position, the nextIndex corresponding to its key is updated accordingly. Once this iteration is completed, we can copy the sorted output array back to the input array.
template <typename T>
void countingSort (vector<T>& inputs, int maxKey) {
vector<int> counter(maxKey+1);
//counter[i] corresponds to the number of entries with key equal to i
for (const auto& input : inputs) counter[input.first]++;
//nextIndex[i] corresponds to the number of entries with key less than i
vector<int> nextIndex(maxKey+1);
std::partial_sum(counter.begin(), counter.end(), nextIndex.begin()+1);
vector<T> output(inputs.size());
for (const auto& input : inputs) output[nextIndex[input.first]++] = input;
std::copy(output.begin(), output.end(), inputs.begin());
}Space optimization
Instead of creating a separate nextIndex array, we can get it modifying the counter array in-place in one pass. The easy way is to initialize nextIndex with the cumulative sum of counter array so that the ith element of nextIndex corresponds to the number of elements with key less or equal than i. We can then build the sorted output iterating backwards through the input array.
template <typename T>
vector<T> countingSort (vector<T> const& inputs, int maxKey) {
vector<int> counter(maxKey+1);
// initialize so that counter[i] corresponds to the number of entries with key equal to i
for (const auto& input : inputs) counter[input.first]++;
// update so that counter[i] corresponds to the number of entries with key less or equal to i
std::partial_sum(counter.begin(), counter.end(), counter.begin());
vector<T> output(inputs.size());
//iterate inputs backwards and use counter to insert element in b sorted
for (auto it = inputs.crbegin(); it != inputs.crend(); ++it) {
output[--counter[it->first]] = *it;
}
return output;
}Conclusion
This post provided an overview of the counting sort algorithm and its C++ implementation. Implementation in other programming languages are available at my github repository.
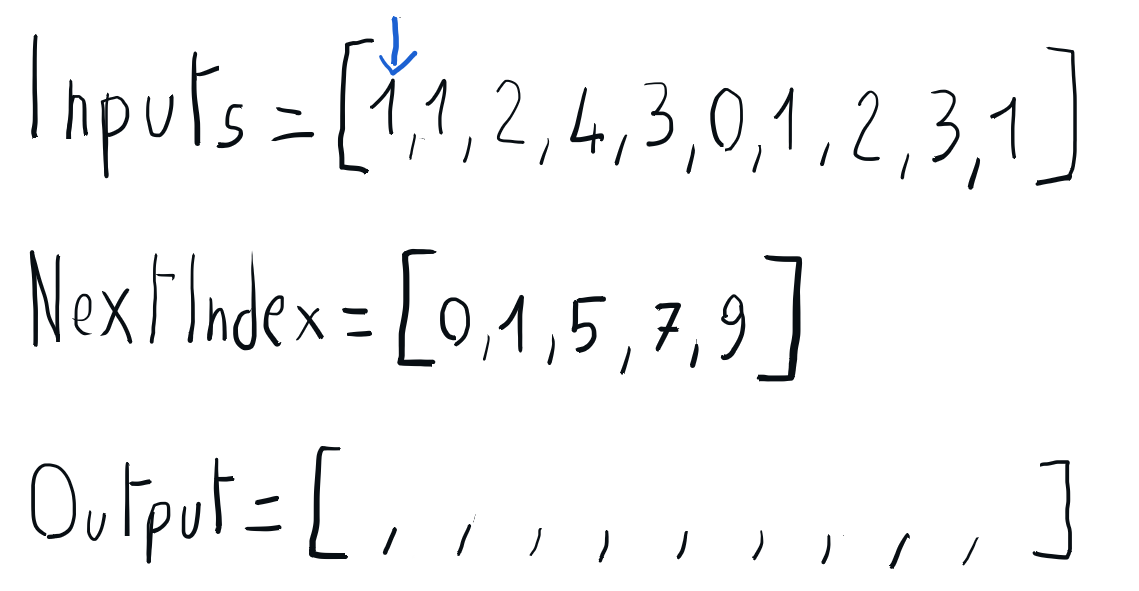
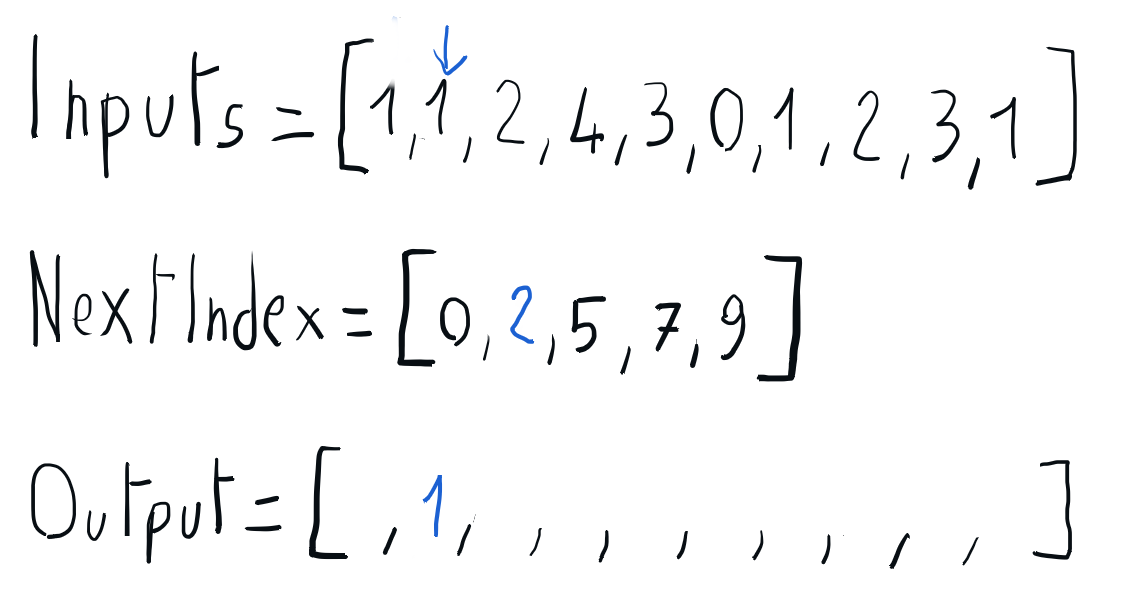
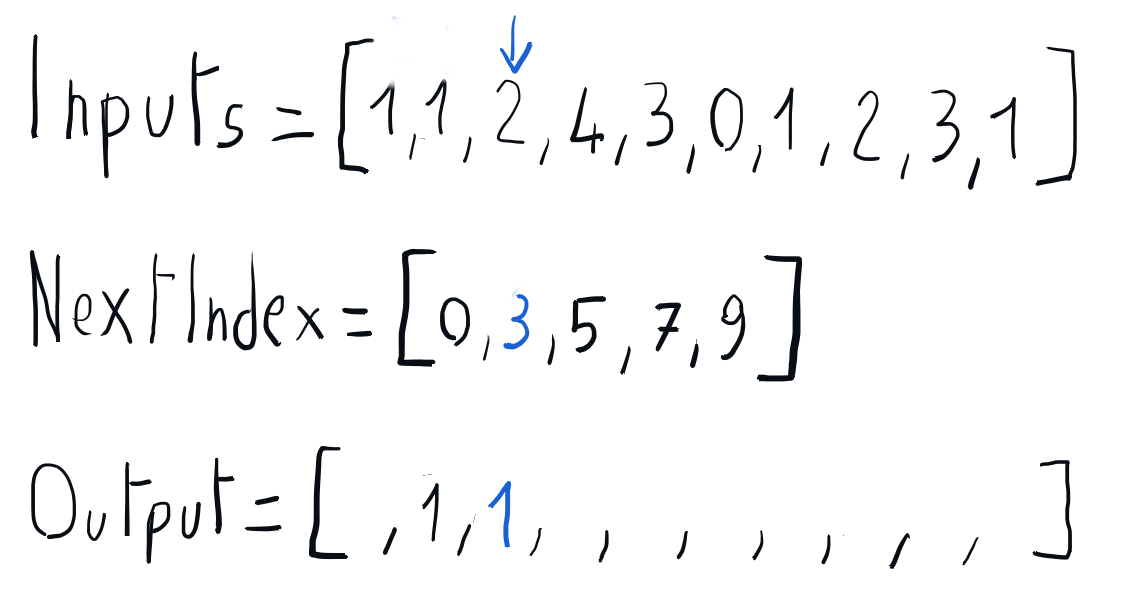
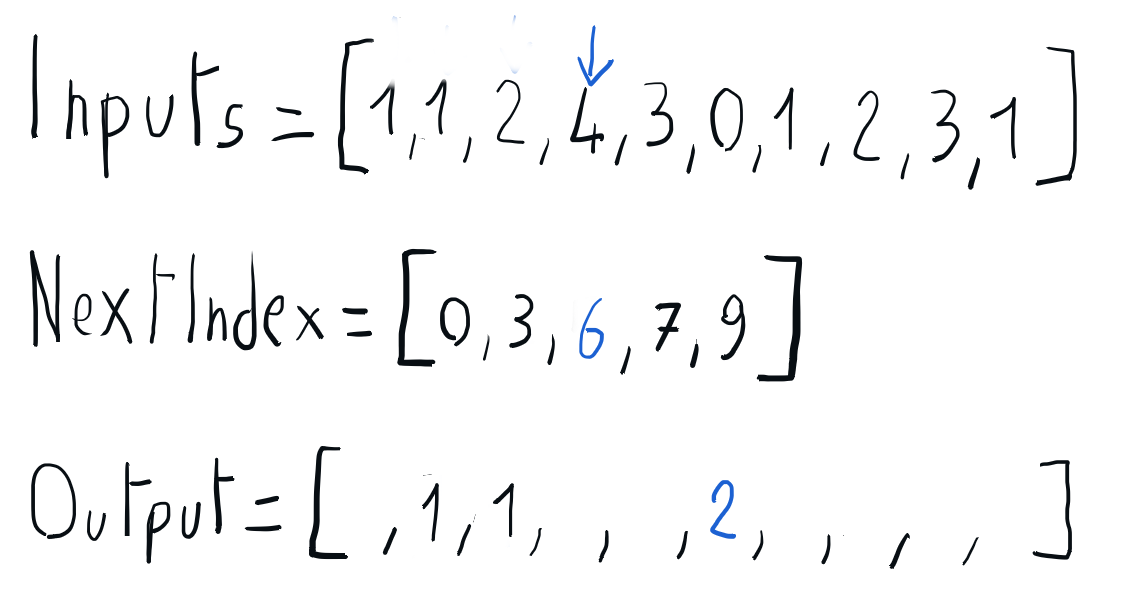
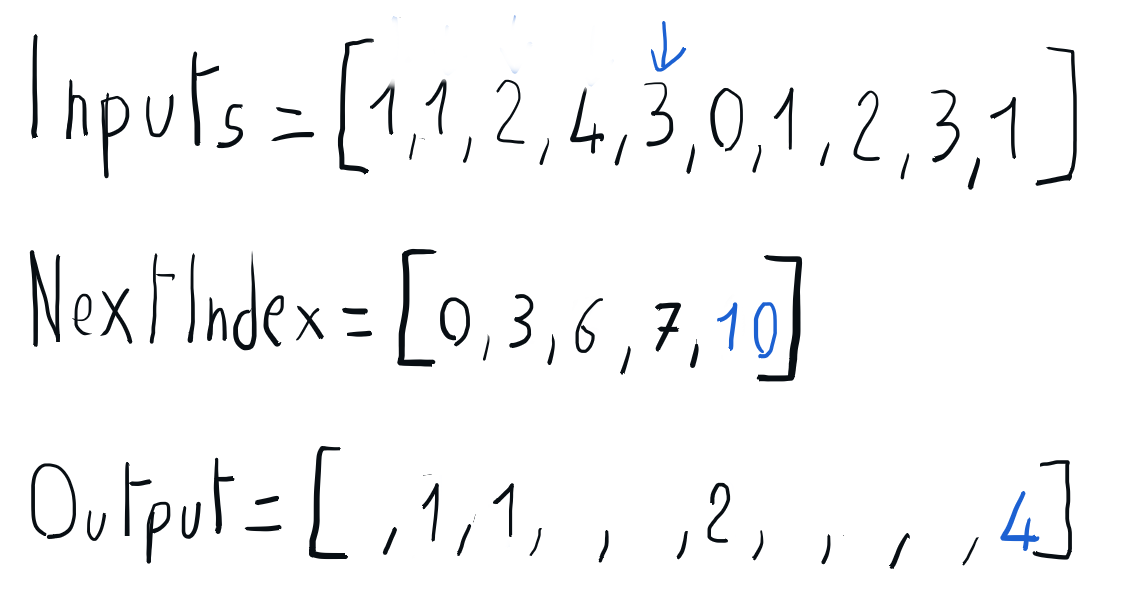
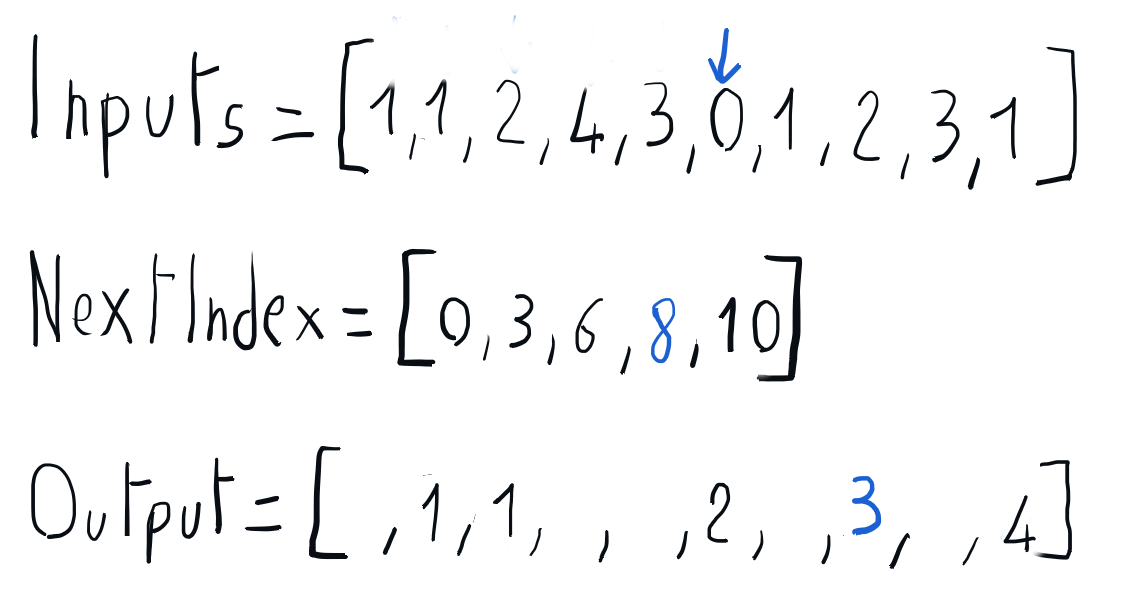
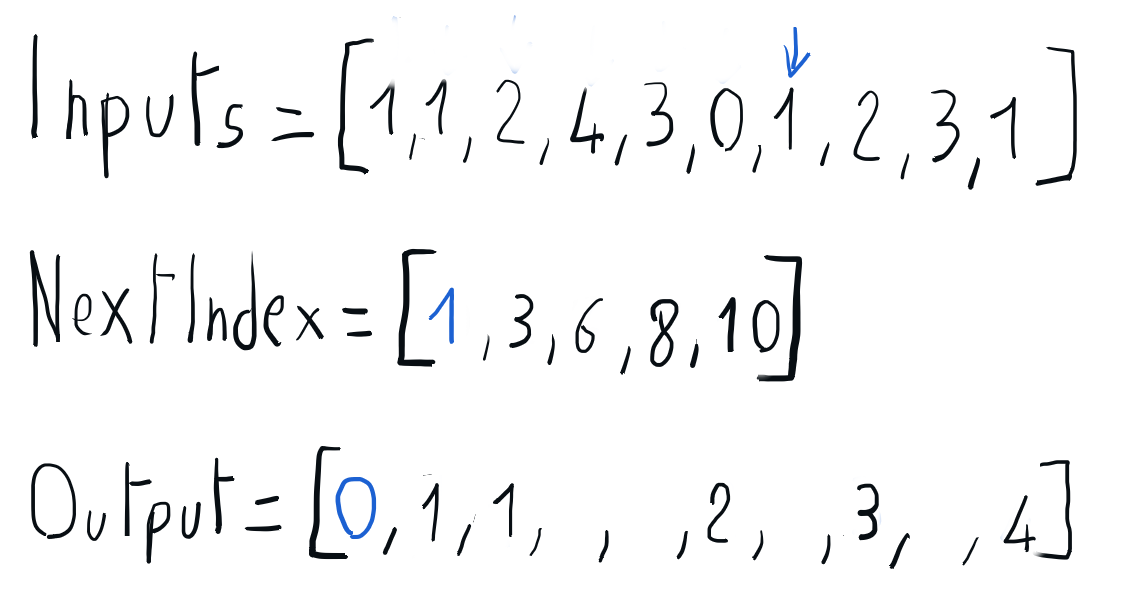
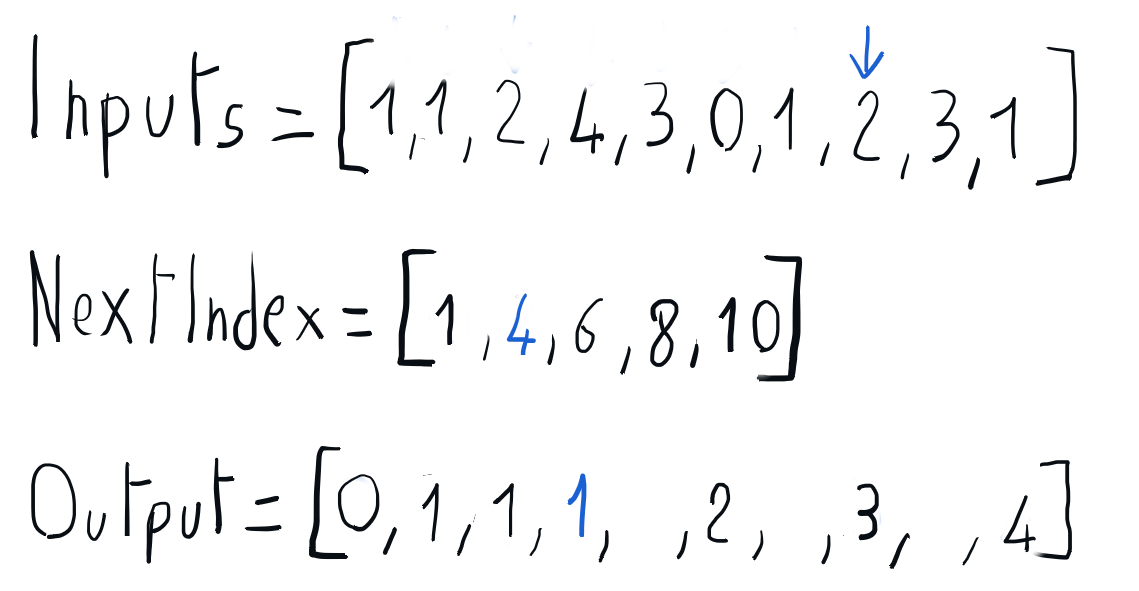
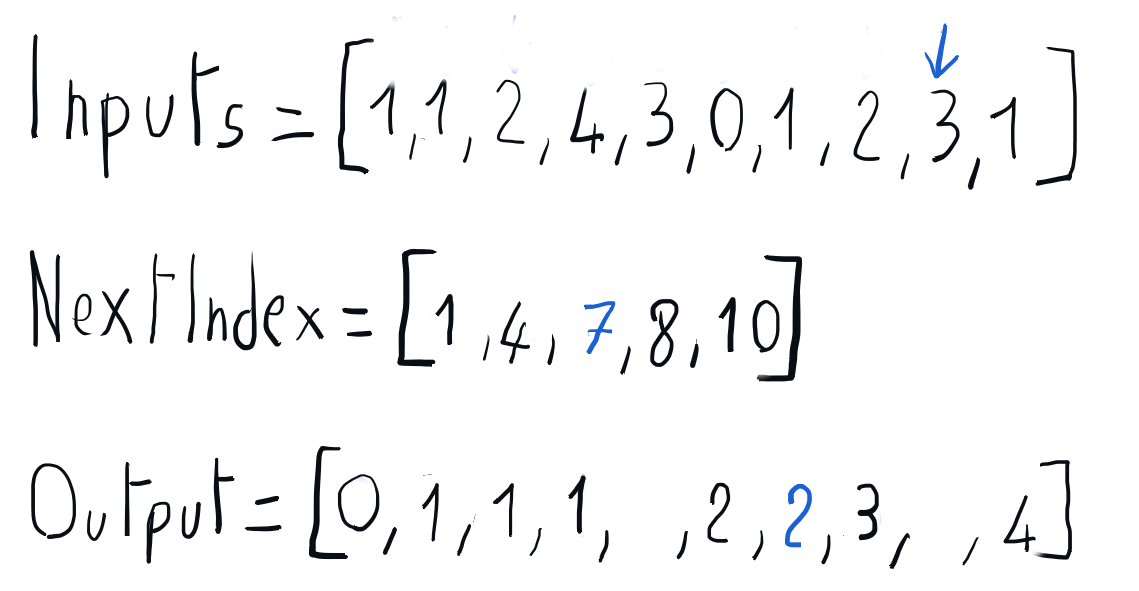
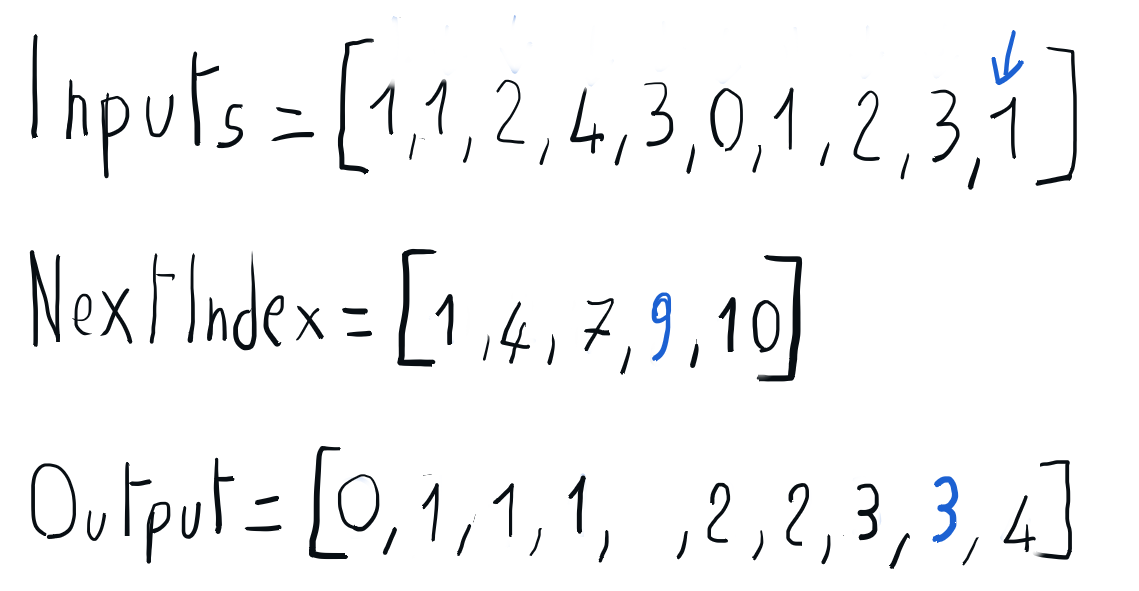
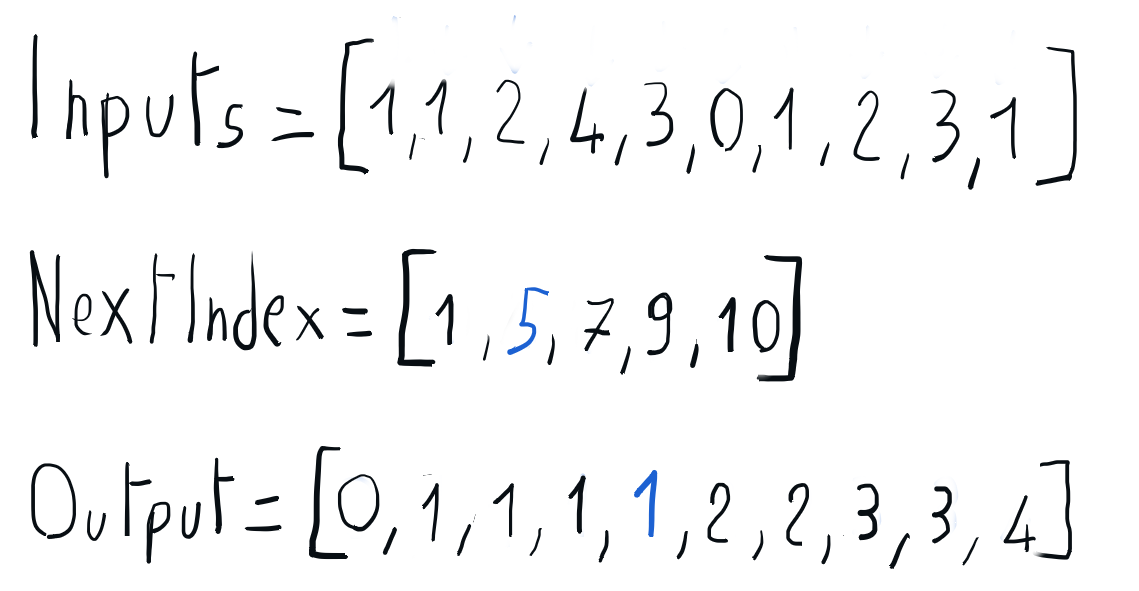
Comments